Problèmes récursifs

Mots

1. Combien de mots peut-on écrire avec 1, 2, 3 lettres ?
2. On note $M(n)$ le nombre de mots qu’on peut écrire avec $n$ lettres. Exprimer $M(n)$ en fonction de $M(n-1)$.
3. Donner une formule close pour $M(n)$ (i.e., une formule non-récursive).
4. En général, avec un alphabet de $k$ lettres, combien de mots de longueur $n$ peut-on écrire ?
5. Écrire un programme (en C, Java, ou tout autre langage) qui prend en entrée un entier $n$ et qui affiche à l’écran tous les mots de $n$ lettres.

Le jeu de Nim

Dans le jeu de Nim, un certain nombre de bâtons sont disposées en rang devant deux joueurs. Chaque joueur, à tour de rôle, choisit de prendre 1, 2 ou 3 bâtons. Celui qui prend le dernier bâton a perdu.

1. Qui gagne si la position de départ comporte 1, 2, 3, 4 ou 5 bâtons ?

À partir de maintenant on va appeler gagnante une position à partir de laquelle le joueur qui joue a une stratégie gagnante, perdante une à partir de laquelle le joueur qui joue perd forcément.

1. Montrer que si $n$ est une position perdante, $n+1$, $n+2$ et $n+3$ sont des positions gagnantes.
2. Montrer que si $n$ est une position perdante, $n+4$ l’est aussi.
3. Donner une formule arithmétique caractérisant les positions perdantes/gagnantes.
4. Prouver la formule précédente par induction.

Triominos

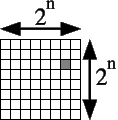
On appelle un échiquier à trou de rang $n$ un plateau composé de $2^n \times 2^n$ cases, dont une des cases a été enlevée. Un échiquier à trou de rang 1 comporte donc 3 cases et un trou. Un échiquier à trou de rang 3 est représenté sur la figure ci-dessous.

Un triomino en « L » est un bloc de trois carrés de la forme (ou toute autre rotation de la pièce… comme au tetris !).

1. Est-il possible de paver tous les échiquiers de rang 1, 2, 3 ?
2. Est-il toujours possible de paver un échiquier à trou à l’aide de triominos ?

Tour de Hanoi

Le jeu de la tour de Hanoï à été inventé par le mathématicien Édouard Lucas. Il le décrit ainsi dans le journal Récréations mathématiques en 1892:

N. Claus de Siam a vu, dans ses voyages pour la publication des écrits de l’illustre Fer-Fer-Tam-Tam, dans le grand temple de Bénarès, au-dessous du dôme qui marque le centre du monde, trois aiguilles de diamant, plantées dans une dalle d’airain, hautes d’une coudée et grosses comme le corps d’une abeille. Sur une de ces aiguilles, Dieu enfila au commencement des siècles, 64 disques d’or pur, le plus large reposant sur l’airain, et les autres, de plus en plus étroits, superposés jusqu’au sommet. C’est la tour sacrée du Brahmâ. Nuit et jour, les prêtres se succèdent sur les marches de l’autel, occupés à transporter la tour de la première aiguille sur la troisième, sans s’écarter des règles fixes que nous venons d’indiquer, et qui ont été imposées par Brahma. Quand tout sera fini, la tour et les brahmes tomberont, et ce sera la fin des mondes!

Voici l’image d’une tour de Hanoï miniature

En sythèse, les brahmes ont droit de déplacer un seul disque à la fois d’une aiguille à une autre, à condition de ne pas poser un disque plus gros sur un plus petit. Leur but est de transporter toute la tour sur la troisième aiguille.

1. Donner une solution pour déplacer une tout composée de seulement, 1, 2, 3 ou 4 disques.
2. Donner une solution pour une tour composée de $n$ disques.
3. On note $H(n)$ le nombre de coups nécessaires à déplacer une tour de $n$ disques. Exprimer $H(n)$ en fonction de $H(n-1)$.
4. Donner une formule close pour $H(n)$.

Partitions

On cherche à calculer le nombre maximum de parts de pizza que l’on peut obtenir en effectuant $n$ coupes droites dans une pizza. Peu importe la taille ou la forme des parts. Appelons ce nombre $P(n)$.

1. Calculer $P(0)$, $P(1)$, $P(2)$, $P(3)$ à la main.
2. Si l’on a déjà effectué n coupes, quelle est la meilleure stratégie pour placer la coupe $n + 1$ afin de maximiser le nombre de parts créées ?
3. Exprimer $P(n+1)$ en fonction de $P(n)$.
4. Donner une formule close pour $P(n)$.